Examples

Some circuits, protocols and sampling

In this section, we show more examples of quantum protocols and sampling outcomes for both direct MC and subset sampling. All examples are also described in more detail in the linked paper.

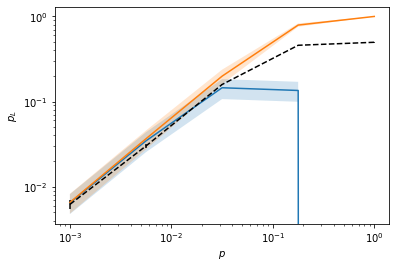
1. GHZ state preparation

See sections 1C and 3B in paper

# Sampling parameters

sample_range = np.logspace(-3,0,5)
err_params = {'q': sample_range}
err_model = qs.noise.S1
CHP = qs.StabilizerSimulator
p_max = {'q': 1e-3}

# Direct MC sampling

print("--- Direct MC sampling ---")

mc_sam = qs.DirectSampler(ghz1, CHP, err_params=err_params, err_model=err_model)
mc_sam.run(10_000)

print("--- Subset sampling ---")

ss_sam = qs.SubsetSampler(protocol=ghz1, simulator=CHP,  p_max=p_max, err_model=err_model, err_params=err_params, L=1)
ss_sam.run(1_000)

# Plot results

p_L, std = mc_sam.stats()
p_L_low, ss_std_low, p_L_up, ss_std_up = ss_sam.stats()

plt.errorbar(sample_range, p_L, fmt='--', c="black", yerr=std, label="Direct MC")
plt.loglog(sample_range, p_L_low, label='SS low')
plt.fill_between(sample_range, p_L_low-ss_std_low, p_L_low+ss_std_low, alpha=0.2)
plt.loglog(sample_range, p_L_up, label='SS low')
plt.fill_between(sample_range, p_L_up-ss_std_up, p_L_up+ss_std_up, alpha=0.2)
plt.ylabel('$p_L$')
plt.xlabel('$p$')

--- Direct MC sampling ---

--- Subset sampling ---

Text(0.5, 0, '$p$')

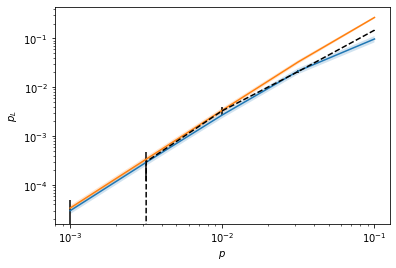
2. Deterministic fault-tolerant preparation of Steane code state

See section 3C in paper

# Sampling parameters

sample_range = np.logspace(-3,-1,5)
err_params = {'q1': sample_range/10, 'q2': sample_range}
err_model = qs.noise.S2
CHP = qs.StabilizerSimulator
p_max = {'q1': 1e-3, 'q2': 1e-2}

# Direct MC sampling

print("--- Direct MC sampling ---")

mc_sam = qs.DirectSampler(steane0, CHP, err_params=err_params, err_model=err_model)
mc_sam.run(10_000)

print("--- Subset sampling ---")

ss_sam = qs.SubsetSampler(steane0, CHP,  p_max=p_max, err_model=err_model, err_params=err_params, L=4)
ss_sam.run(10_000)

# Plot results

p_L, std = mc_sam.stats()
p_L_low, ss_std_low, p_L_up, ss_std_up = ss_sam.stats()

plt.errorbar(sample_range, p_L, fmt='--', c="black", yerr=std, label="Direct MC")
plt.loglog(sample_range, p_L_low, label='SS low')
plt.fill_between(sample_range, p_L_low-ss_std_low, p_L_low+ss_std_low, alpha=0.2)
plt.loglog(sample_range, p_L_up, label='SS low')
plt.fill_between(sample_range, p_L_up-ss_std_up, p_L_up+ss_std_up, alpha=0.2)
plt.ylabel('$p_L$')
plt.xlabel('$p$')

--- Direct MC sampling ---

--- Subset sampling ---

Text(0.5, 0, '$p$')

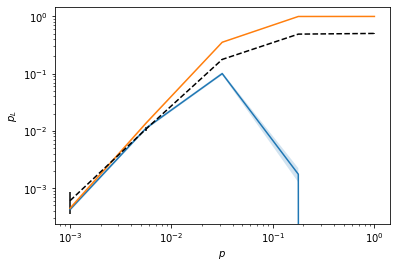
3. Flag-FT stabilizer \(|0\rangle_L\) measurement

See section 3D in paper

# Sampling parameters

sample_range = np.logspace(-3,0,5)
err_params = {'q': sample_range}
err_model = qs.noise.S1
CHP = qs.StabilizerSimulator
p_max = {'q': 1e-2}

# Direct MC sampling

print("--- Direct MC sampling ---")

mc_sam = qs.DirectSampler(flagstab, CHP, err_params=err_params, err_model=err_model)
mc_sam.run(10_000)

print("--- Subset sampling ---")

ss_sam = qs.SubsetSampler(flagstab, CHP,  p_max=p_max, err_model=err_model, err_params=err_params, L=8)
ss_sam.run(10_000)

# Plot results

p_L, std = mc_sam.stats()
p_L_low, ss_std_low, p_L_up, ss_std_up = ss_sam.stats()

plt.errorbar(sample_range, p_L, fmt='--', c="black", yerr=std, label="Direct MC")
plt.loglog(sample_range, p_L_low, label='SS low')
plt.fill_between(sample_range, p_L_low-ss_std_low, p_L_low+ss_std_low, alpha=0.2)
plt.loglog(sample_range, p_L_up, label='SS low')
plt.fill_between(sample_range, p_L_up-ss_std_up, p_L_up+ss_std_up, alpha=0.2)
plt.ylabel('$p_L$')
plt.xlabel('$p$')

--- Direct MC sampling ---

--- Subset sampling ---

Text(0.5, 0, '$p$')